Standard Deviation Guide: Understanding the Basics in 2026
Standard deviation is the backbone of modern statistics, yet it remains one of the most misunderstood concepts among students and professionals alike. Its influence stretches far beyond textbooks, shaping decisions in finance, science, and even our daily lives.
Understanding standard deviation in 2026 is essential for anyone who works with data. Whether you are analyzing investment risks, evaluating scientific experiments, or making everyday choices, a clear grasp of this concept can set you apart.
Mastery of standard deviation unlocks the ability to interpret data accurately and make informed, competitive decisions. Are you ready to gain the clarity you need?
This guide demystifies standard deviation, offering a step-by-step approach to its basics, calculations, and practical uses. Explore what standard deviation truly means, how to calculate it, where it matters most, and the pitfalls to avoid.
What Is Standard Deviation?
Understanding standard deviation is essential for anyone working with data in 2026. This statistic helps us see how much values in a set differ from the average, making it a cornerstone of meaningful data analysis.
Definition and Core Concept
Standard deviation measures how spread out the numbers in a data set are. At its core, standard deviation shows the average distance of each value from the mean, giving you insight into how consistent or variable your data is. If all values are close to the mean, the standard deviation will be low. If the values are more spread out, the standard deviation will be higher.
To understand standard deviation, it helps to compare it with other concepts. The mean is simply the average of your data. Variance, on the other hand, is the average of the squared differences from the mean. Standard deviation is the square root of variance, bringing the measure back to the original units of the data, which makes it more practical for interpretation.
There are two main types of standard deviation: population and sample. Population standard deviation is used when you have data for an entire group. Sample standard deviation applies when you analyze a subset of the group, using a slightly different formula to account for the smaller size.
Why does standard deviation matter so much? It quantifies the typical difference between each data point and the mean, making it vital for comparing consistency across data sets. For example, in education, it helps teachers understand the spread of student test scores. In science, it reveals variability in experimental results. In finance, it indicates how much investment returns might fluctuate.
Common misconceptions about standard deviation include confusing it with variance or the range. Unlike the range, which only considers the highest and lowest values, standard deviation uses every data point for a complete picture of variability.
Here’s a table summarizing how standard deviation applies across different fields:
| Example Type | Data Set | Mean | Standard Deviation Purpose |
|---|---|---|---|
| Test Scores | 80, 85, 90, 95, 100 | 90 | Measures score consistency |
| Daily Temperatures | 68, 70, 72, 74, 76 | 72 | Tracks weather variability |
| Investment Returns | 5%, 7%, 9%, 11%, 13% | 9% | Assesses return volatility |
For a deeper look at how standard deviation is used to interpret student performance, see Standard deviation in educational data analysis.
In short, standard deviation answers the question: “How much do the values in my data set typically differ from the average?”
Historical Context and Evolution
The concept of standard deviation has a rich history, stretching back to the 19th century. Its roots can be traced to the work of mathematicians who sought ways to measure error and variability in data. Karl Pearson, a pioneer in statistics, played a key role in formalizing standard deviation as a mathematical tool.
As technology advanced, calculating standard deviation became far more accessible. Early statisticians performed calculations by hand, but today’s analysts use spreadsheets, statistical software, and even AI-driven platforms to process massive data sets in seconds.
In 2026, standard deviation is more relevant than ever. Modern data science and analytics rely on this measure to interpret complex patterns, identify trends, and make predictions. In financial markets, standard deviation is a primary indicator of risk and volatility, guiding investment strategies and portfolio management. Scientists use it to assess experimental reliability and reproducibility, while educators depend on it for measuring student performance.
Moreover, standard deviation has become central in machine learning and artificial intelligence. Algorithms frequently use this statistic to normalize data, detect anomalies, and improve the accuracy of predictive models.
Throughout its evolution, standard deviation has remained a fundamental measure of variability, adapting to new challenges and technologies. Whether you are analyzing stock prices, monitoring climate trends, or evaluating medical studies, understanding standard deviation equips you to make informed decisions based on data.
The Mathematical Foundation of Standard Deviation
Understanding the mathematical foundation of standard deviation is essential for anyone working with data in 2026. This section breaks down the formula, its components, and how standard deviation connects to other core statistical measures.

Understanding the Formula
The standard deviation formula is the cornerstone of statistical analysis. For a population, the formula is:
SD = sqrt(Σ(x – μ)² / N)
Here, SD stands for standard deviation, x represents each data point, μ is the mean, and N is the total number of data points. For sample data, the formula slightly changes:
SD = sqrt(Σ(x – x̄)² / (n – 1))
In this case, x̄ is the sample mean, and n is the sample size. The denominator is n–1 rather than N to account for sample bias, a correction known as Bessel’s correction.
Let’s see how this works in practice. Given the data set 6, 2, 3, 1:
| Data Point | Deviation from Mean | Squared Deviation |
|---|---|---|
| 6 | 6 – 3 = 3 | 9 |
| 2 | 2 – 3 = -1 | 1 |
| 3 | 3 – 3 = 0 | 0 |
| 1 | 1 – 3 = -2 | 4 |
Sum of squared deviations: 9 + 1 + 0 + 4 = 14
For a population, divide by N (4): 14 / 4 = 3.5
Standard deviation is the square root of variance: sqrt(3.5) ≈ 1.87
A key property is that standard deviation is always non-negative and uses the same units as the data. This makes interpretation straightforward, especially compared to variance, which is expressed in squared units. Standard deviation helps quantify typical differences from the mean, providing clear insight into data spread.
Relationship to Other Statistical Measures
Standard deviation is only one way to measure data dispersion. It is closely related to variance, which is simply the square of standard deviation. While variance gives a sense of spread, its squared units can make interpretation challenging. Standard deviation overcomes this by returning to the original units.
Comparing standard deviation with other measures:
| Measure | Definition | Units | Best For |
|---|---|---|---|
| Standard Deviation | Average distance from mean | Original units | Normal, symmetric data |
| Variance | Mean of squared deviations | Squared units | Theoretical calculations |
| Range | Max value – Min value | Original units | Quick spread estimate |
| Interquartile Range | Q3 – Q1 (middle 50% of data) | Original units | Skewed or outlier-prone data |
Standard deviation is particularly useful when data follows a bell-shaped, or normal, distribution. In these cases, the empirical rule (or 68–95–99.7 rule) states that about 68% of data falls within one standard deviation of the mean, 95% within two, and 99.7% within three.
When deciding which measure to use, consider the data’s shape and presence of outliers. Standard deviation works best for symmetric, bell-shaped data, while the interquartile range is better for skewed distributions.
In summary, standard deviation is a versatile tool, connecting the concepts of mean, variance, and broader measures of spread. Understanding its mathematical foundation lays the groundwork for deeper analysis and more informed decisions.
Step-by-Step Guide: Calculating Standard Deviation
Understanding how to calculate standard deviation is essential for anyone looking to interpret data with confidence. Whether you are analyzing test scores, daily temperatures, or financial returns, this step-by-step guide will walk you through the process in a clear and structured way.
Accurate calculation of standard deviation is not just a mathematical exercise. It is a critical factor in risk assessment, especially in fields like finance where risk-weighted assets explained depend on understanding variability and volatility. Let us break down the process, so you can apply it to any data set with ease.
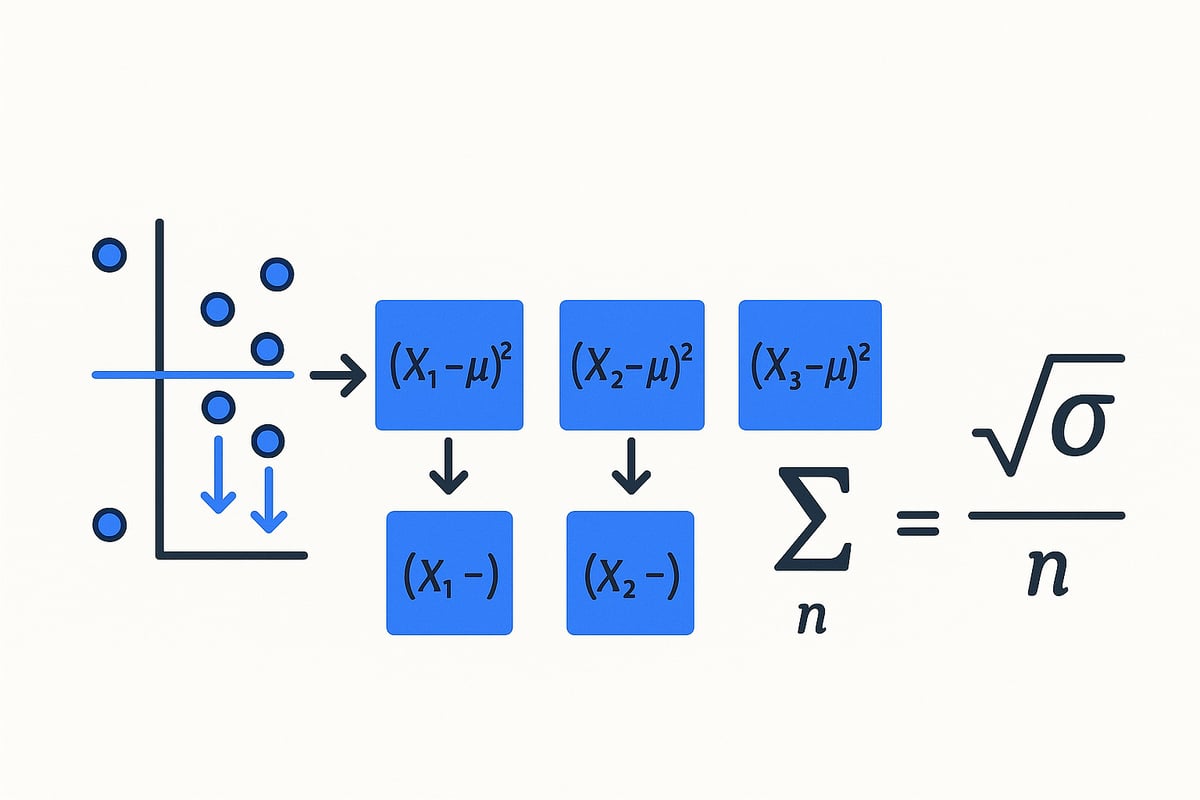
Step 1: Find the Mean
The first step in calculating standard deviation is to determine the mean, or average, of your data set. The mean serves as the central reference point from which all deviations are measured.
To calculate the mean, sum all data points and divide by the total number of values. For example, consider the data set: 6, 2, 3, 1.
Mean = (6 + 2 + 3 + 1) / 4 = 12 / 4 = 3
This mean will be used in all subsequent steps. Ensuring accuracy at this stage is crucial, as any error here will affect the entire standard deviation calculation. Double-check your arithmetic before moving forward.
Step 2: Calculate Deviations from the Mean
Now, subtract the mean from each data point to find the deviation for each value. Deviations can be positive or negative, depending on whether the data point is above or below the mean.
Here is a table to illustrate:
| Data Point | Mean | Deviation (Data - Mean) |
|---|---|---|
| 6 | 3 | 6 - 3 = 3 |
| 2 | 3 | 2 - 3 = -1 |
| 3 | 3 | 3 - 3 = 0 |
| 1 | 3 | 1 - 3 = -2 |
This step reveals how far each data point is from the average. Recording both the data and their deviations helps prevent calculation errors and prepares your data for the next stage.
Step 3: Square Each Deviation
To eliminate negative values and emphasize larger differences, square each deviation. Squaring ensures that all values are positive and magnifies any outliers.
Let us continue with our example:
| Data Point | Deviation | Squared Deviation |
|---|---|---|
| 6 | 3 | 9 |
| 2 | -1 | 1 |
| 3 | 0 | 0 |
| 1 | -2 | 4 |
At this point, you have transformed the deviations into squared deviations. This makes it easier to aggregate the variability in the data set for the next step.
Step 4: Sum the Squared Deviations
Next, add up all the squared deviations. This total forms the numerator in the variance calculation, which is a key step toward finding the standard deviation.
Sum of squared deviations: 9 + 1 + 0 + 4 = 14
This sum quantifies the total dispersion of your data points from the mean. It is important to check your work here to ensure all squared deviations have been included correctly.
Step 5: Divide by the Number of Data Points (or n–1)
Now, divide the sum of squared deviations by the number of data points if you are working with a population, or by n–1 if you are calculating a sample standard deviation. The use of n–1, known as Bessel's correction, provides an unbiased estimate when dealing with samples.
For our example (population standard deviation):
Variance = 14 / 4 = 3.5
If you were calculating the sample standard deviation, you would divide by 3 instead of 4. Understanding when to use each denominator is vital for accurate results.
Step 6: Take the Square Root
The final calculation step is to take the square root of the variance. This brings your result back to the same units as your original data, making the standard deviation easy to interpret.
For our example:
Standard deviation = √3.5 ≈ 1.87
This value tells you how much, on average, each data point deviates from the mean. A lower standard deviation indicates that data points are closely clustered, while a higher value suggests more variability.
Step 7: Practice Example
Let us apply the process to a new set: 1, 4, 7, 2, 6.
Step 1: Mean = (1 + 4 + 7 + 2 + 6) / 5 = 20 / 5 = 4
Step 2: Deviations: 1-4 = -3, 4-4 = 0, 7-4 = 3, 2-4 = -2, 6-4 = 2
Step 3: Squared deviations: 9, 0, 9, 4, 4
Step 4: Sum = 9 + 0 + 9 + 4 + 4 = 26
Step 5: Variance (population) = 26 / 5 = 5.2
Step 6: Standard deviation = √5.2 ≈ 2.28
This example demonstrates how each step leads to a result that reflects the spread of the data set. Always round your answer appropriately and interpret the standard deviation in the context of your data.
Common Calculation Mistakes and How to Avoid Them
Even experienced analysts can make mistakes when calculating standard deviation. Common errors include forgetting to square deviations, using the wrong denominator, and making rounding errors at each step.
To avoid these pitfalls:
- Always double-check each calculation, especially when squaring deviations.
- Confirm you are using the correct denominator (N for population, n–1 for sample).
- Use precise rounding rules, and do not round intermediate results prematurely.
- For large or complex data sets, consider using spreadsheet functions or statistical software, but understand the manual steps for deeper insight.
By following these guidelines, you will minimize errors and ensure your standard deviation results are reliable and meaningful.
Interpreting and Applying Standard Deviation in 2026
Understanding how to interpret standard deviation is essential for anyone working with data in 2026. This metric goes beyond calculation, offering deep insights into patterns, consistency, and risk across various fields. By mastering how standard deviation applies to real-world scenarios, you can make smarter decisions and avoid common analytical pitfalls.

What Standard Deviation Tells You About Data
Standard deviation is a powerful lens for viewing the consistency or variability within a dataset. A low standard deviation signals that most values cluster closely around the mean, while a high standard deviation reveals wide variation. For example, if two classrooms have the same average test score but different standard deviations, the one with the lower value indicates students performed more uniformly.
In finance, a stable investment portfolio is characterized by a lower standard deviation, meaning returns are predictable. In quality control, manufacturers rely on standard deviation to monitor product consistency, ensuring items meet required specifications. In education, instructors use standard deviation to assess whether test results reflect consistent student understanding or if further review is needed.
| Scenario | Low SD (Consistent) | High SD (Variable) |
|---|---|---|
| Test Scores | Most students score similarly | Scores widely scattered |
| Daily Temperatures | Little change day-to-day | Big swings in readings |
| Investment Returns | Predictable profits | Unstable, risky returns |
By interpreting standard deviation in context, you can identify trends, spot anomalies, and make informed choices in any data-driven environment.
Standard Deviation and the Normal Distribution
The relationship between standard deviation and the normal distribution is central to statistical analysis. In a normal distribution, data points cluster symmetrically around the mean, forming the classic bell curve. The standard deviation sets the scale for this spread, defining how much data deviates from the center.
The empirical rule, also known as the 68-95-99.7 rule, states that approximately 68% of values fall within one standard deviation of the mean, 95% within two, and 99.7% within three. This makes standard deviation invaluable for probability assessments and risk evaluations.
Consider height measurements in a population. If the mean height is 170 cm and the standard deviation is 6 cm, most individuals will measure between 164 and 176 cm. When analyzing datasets, understanding this rule helps you quickly gauge the likelihood of extreme values and assess whether results are typical or unusual.
Standard Deviation in Financial Markets
In financial markets, standard deviation is synonymous with risk and volatility. Investors and analysts use it to measure how much asset returns fluctuate over time. A stock or portfolio with a high standard deviation is considered risky, as its value can swing dramatically from the mean.
For example, the annualized standard deviation of S&P 500 returns is a key indicator of market turbulence. Standard deviation is also a cornerstone of modern portfolio theory, guiding asset allocation to balance expected returns against risk. Algorithmic trading systems and AI-powered analytics rely on standard deviation to identify opportunities and avoid excessive risk.
Understanding volatility is crucial for evaluating investment strategies and theories like the Efficient market hypothesis overview, which depends on accurate measurements of market unpredictability.
Standard Deviation in Science and Research
In science and research, standard deviation plays a critical role in evaluating experimental error and reproducibility. When researchers conduct experiments, they use standard deviation to understand how much measurements vary from the average, revealing the reliability of their results.
For instance, in clinical trials, a low standard deviation in patient outcomes suggests that a treatment consistently produces similar effects. High standard deviation might indicate uncontrolled variables or inconsistent responses. Reporting standard deviation alongside mean values helps other scientists assess the significance and credibility of findings.
Statistical significance tests, such as the t-test, incorporate standard deviation to determine whether results differ enough to rule out random chance. Mastering its interpretation is essential for drawing valid scientific conclusions.
Limitations and When Not to Use Standard Deviation
While standard deviation is a versatile tool, it is not always the best measure of spread. One key limitation is its sensitivity to outliers. Extreme values can inflate the standard deviation, distorting the true variability of most data points. In highly skewed distributions, standard deviation may give a misleading impression of consistency.
In cases like income data, where a few individuals earn much more than the majority, the median and interquartile range often provide a clearer picture of typical values. These alternatives are less affected by outliers and skewness. Before relying on standard deviation, always assess your data's distribution and consider whether a different measure might yield more meaningful insights.
Understanding when to use standard deviation and when to opt for alternatives ensures your analysis remains accurate and relevant. This awareness is especially important as data complexity grows in 2026, making careful interpretation a necessary skill for every analyst.
Advanced Insights: Standard Deviation in Modern Data Analysis
In 2026, standard deviation remains a cornerstone for understanding variability in massive, complex data sets. As data streams grow exponentially, professionals rely on this metric for quick, actionable insights across industries. Let us explore how standard deviation adapts in modern analytics, its relationship to other measures, and the tools that make it accessible to everyone.
Standard Deviation and Big Data
With the explosion of big data, calculating standard deviation on vast data sets is now routine in real time. Modern platforms like Python’s Pandas, R, and advanced spreadsheets automate these calculations, allowing analysts to focus on interpretation rather than manual computation.
For example, in the Internet of Things (IoT), standard deviation helps monitor sensor consistency across millions of data points each second. AI-driven algorithms use standard deviation to flag anomalies, ensuring rapid responses to unusual patterns. In cloud-based analytics, standard deviation enables scalable quality control, informing business decisions instantly.
As a result, standard deviation empowers organizations to manage uncertainty, optimize performance, and ensure data-driven accuracy at scale.
Standard Deviation vs. Alternative Measures
While standard deviation is widely used, it is not always the best choice for every data set. Alternatives like mean absolute deviation (MAD) and the interquartile range (IQR) offer robust measures for skewed or outlier-prone data. For example, income distributions often require IQR to avoid distortion from extreme values.
Robust statistics, such as S_n and Q_n, further improve resistance to anomalies. If you want to explore these options in detail, see this guide on robust measures of scale.
Choosing between standard deviation and its alternatives depends on your data’s shape and the insights you seek. Always match the measure to your analysis goals for accurate interpretation.
Confidence Intervals and Standard Error
Standard deviation is essential for building confidence intervals and calculating standard error, both crucial for statistical inference. The standard error uses standard deviation to estimate how much a sample mean might differ from the true population mean.
For example, when polling voter intentions, analysts might report a margin of error, which depends directly on the sample’s standard deviation. This margin helps communicate the reliability of survey results to the public.
Understanding how standard deviation underpins confidence intervals allows you to judge the trustworthiness of research findings and make better-informed decisions.
Mathematical Properties and Theorems
Standard deviation has unique mathematical properties that support its widespread use. Chebyshev’s inequality guarantees that a minimum percentage of data falls within a set number of standard deviations from the mean, regardless of distribution shape.
Scaling data by a constant affects standard deviation proportionally, while shifting data leaves it unchanged. In geometry, standard deviation represents the average distance from the mean in Euclidean space. For those interested in effect size and geometric perspectives, the geometric standardized mean difference provides additional context.
Mastering these properties enhances your ability to apply standard deviation confidently in diverse analytical tasks.
Rapid Calculation Methods and Tools
Advancements in technology have made standard deviation calculation faster and more accessible than ever. Software packages like Excel, SPSS, and cloud-based analytics platforms offer one-click solutions for both simple and weighted standard deviation.
For large or weighted data sets, formulas can be implemented using code:
import numpy as np
data = [1, 2, 3, 4, 5]
weights = [1, 2, 1, 1, 2]
weighted_sd = np.sqrt(np.average((data - np.average(data, weights=weights))**2, weights=weights))
Understanding manual calculation steps is still valuable, but leveraging modern tools ensures accuracy and efficiency, especially when analyzing big data with standard deviation.
Frequently Asked Questions About Standard Deviation
Understanding standard deviation can be challenging, especially with so many related concepts in statistics. Here are clear answers to the most common questions about standard deviation to help you build a solid foundation and apply it confidently in any field.
What is the difference between variance and standard deviation?
Variance and standard deviation are closely related, but not identical. Variance measures the average squared distance of each data point from the mean, so its units are squared. Standard deviation, on the other hand, is simply the square root of the variance, which means it is expressed in the same units as the original data. This makes standard deviation easier to interpret in practical situations.
Why do we use n–1 for sample standard deviation?
When calculating standard deviation for a sample, we divide by n–1 instead of n to apply what is known as Bessel's correction. This adjustment ensures that the sample standard deviation is an unbiased estimator of the population standard deviation. Using n would tend to underestimate the spread, while n–1 corrects for this and gives a more accurate result when dealing with samples.
When should I use standard deviation over other spread measures?
Standard deviation is most appropriate when your data follows a roughly symmetric, bell-shaped distribution, such as the normal distribution. It excels when you want to understand typical variability around the mean. However, for data with heavy skew or outliers, measures like the interquartile range or median absolute deviation may be more robust than standard deviation.
Can standard deviation be negative?
No, standard deviation can never be negative. Since it is calculated as the square root of the variance, and variance is always positive or zero, standard deviation is always zero or greater. A standard deviation of zero means all values in the dataset are identical, while higher values indicate more spread.
How does standard deviation relate to risk in investing?
In finance, standard deviation is a key measure of risk and volatility. It quantifies how much returns on an investment can vary from the average. A higher standard deviation means greater risk, as returns fluctuate more. Financial analysts often compare standard deviation with other metrics, such as the moving average in finance, to assess trends and volatility together in portfolio analysis.
What tools can help calculate standard deviation in 2026?
Today, and even more so in 2026, there are many tools available to calculate standard deviation efficiently. Spreadsheets like Excel and Google Sheets have built-in functions. Statistical software such as R and Python offer advanced capabilities. Modern analytics platforms and online calculators can compute standard deviation instantly, making analysis accessible to everyone.
How can I interpret a “large” or “small” standard deviation?
The meaning of a large or small standard deviation depends on the context of your data. In general, a large standard deviation means data points are spread out widely from the mean, indicating high variability. A small standard deviation shows data points are clustered closely around the mean, suggesting consistency. Always compare the standard deviation to the mean and the range of the dataset for clearer interpretation.
How does standard deviation help in quality control?
Standard deviation is essential in quality control processes. It helps monitor the consistency of production or service delivery by measuring how much results vary from the average. When standard deviation increases unexpectedly, it may signal a problem that requires investigation. Consistent, low standard deviation means the process is stable and under control.
Now that you have a solid grasp of what standard deviation is and why it matters for understanding data in finance and beyond, you’re ready to take your learning further. Imagine exploring financial markets with interactive charts and AI-powered insights that bring historical context to life—giving you the tools to spot patterns and make smarter decisions. If you’re excited to see how history shapes today’s market movements and want to help shape a platform built for curious minds like yours, join our beta and help us bring history to life.
