Derivative Guide: Mastering Concepts and Applications in 2026

Unlock the transformative potential of the derivative, a concept that is driving innovation across science, engineering, finance, and technology in 2026. Whether you are a student, a professional, or a lifelong learner, this comprehensive guide will illuminate how derivatives shape our understanding of change and motion.

You will discover clear definitions, essential computation rules, and practical examples that connect theory to real-world applications. From mastering foundational principles to exploring the latest trends in calculus and quantitative analysis, each section is designed to build your confidence and expertise.

Ready to master one of mathematics' most powerful tools? Dive in, engage with each section, and let this guide be your pathway to success in today's data-driven world.

Understanding Derivatives: Foundations and Definitions

The derivative is a concept that sits at the heart of mathematics, science, and finance. At its core, a derivative measures how one quantity changes as another changes. In mathematics, it captures the rate at which a function's output shifts as its input varies.

To appreciate the versatility of the derivative, consider its presence in multiple disciplines:

Field	Definition of Derivative
Mathematics	Measures instantaneous rate of change of a function
Linguistics	Word formed from another by derivation (e.g., happiness)
Chemistry	Compound derived from a similar structure (e.g., esters)
Finance	Financial contract deriving value from underlying asset

In mathematics, the derivative is formally defined as the limit of the ratio of the change in a function to the change in its variable, as that change approaches zero. Symbolically, if y = f(x), the derivative is:

f'(x) = lim (h → 0) [f(x + h) - f(x)] / h

The journey of the derivative began in the 15th century, rising to prominence in calculus through the pioneering work of Newton and Leibniz. This breakthrough allowed scholars to describe motion, growth, and change with unprecedented precision.

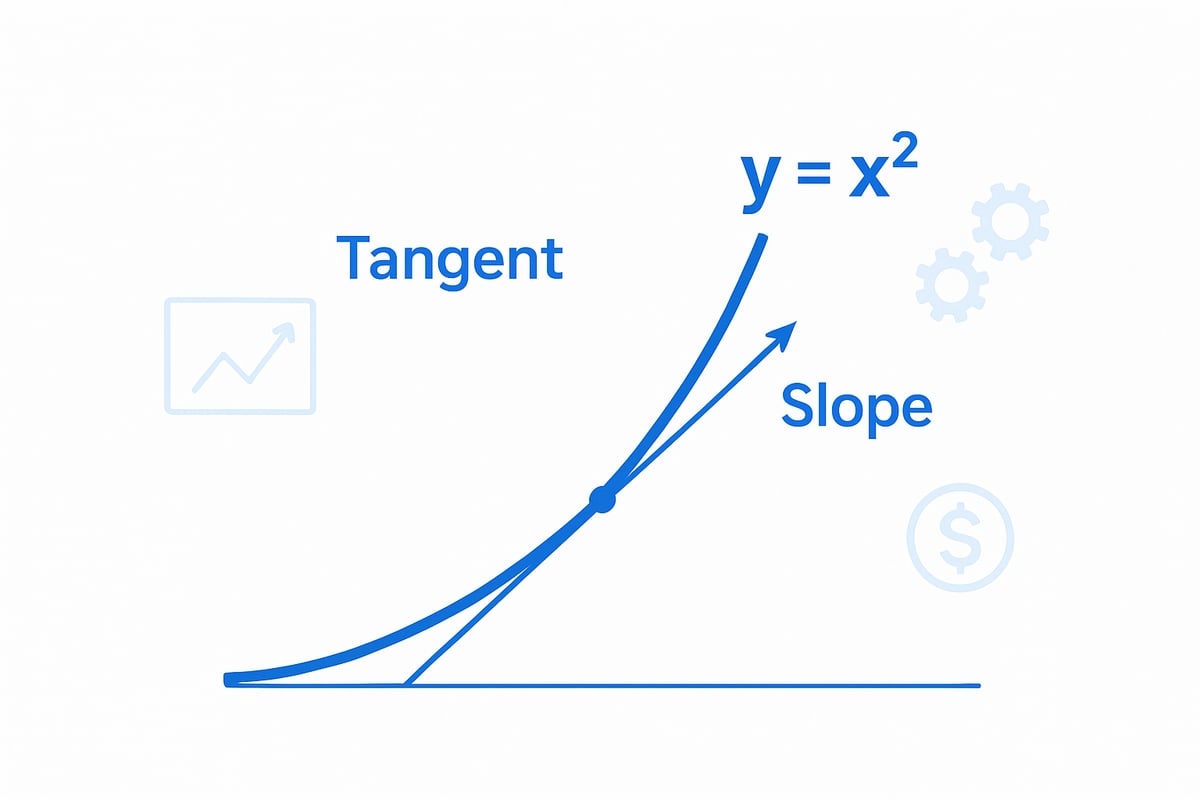
Intuitively, the derivative can be visualized as the slope of a curve at any given point. Imagine tracking a car's speed on a winding road. The derivative tells you exactly how fast the car is moving at each instant, not just over an interval.

Key terminology surrounding the derivative includes:

• Differentiation: The process of finding a derivative.
• Continuity: A function is continuous if it has no sudden jumps.
• Differentiability: A function is differentiable if it has a derivative at every point in its domain.

These concepts are fundamental across many fields. In pure mathematics, the derivative underpins calculus and analysis. In applied sciences and economics, it enables optimization and prediction. For example, the derivative helps economists analyze marginal cost—how much extra cost is incurred by producing one more unit. You can explore more about this in Marginal cost and derivatives.

To see the derivative in action, consider the function y = x². The derivative is 2x, revealing that as x increases, the rate of change accelerates.

In fact, over 80% of STEM fields require a solid grasp of the derivative for foundational coursework. Whether you're modeling population growth, optimizing production, or analyzing financial trends, mastering this concept is essential.

The derivative bridges intuition and analysis, offering a universal language for understanding change. As you progress, you'll see how this single idea powers advancements across disciplines.

Rules of Differentiation: Techniques and Shortcuts

Mastering the rules of differentiation is essential for anyone working with a derivative. These rules transform the process from a tedious calculation into a powerful analytical tool. Whether you are analyzing scientific data, optimizing a business process, or modeling change, knowing these techniques saves time and ensures accuracy.

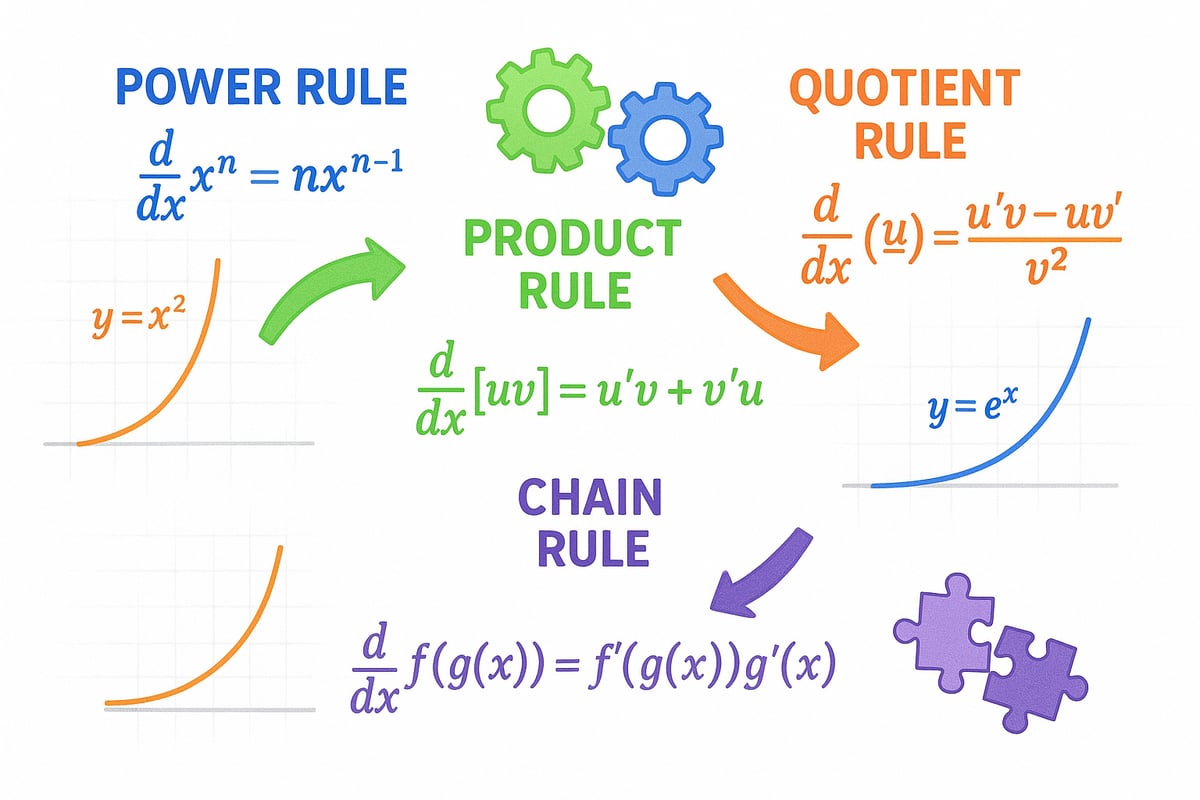
Linearity Rules: Sum and Constant Multiple

Differentiation follows specific linearity properties. The sum rule states that the derivative of a sum is the sum of the derivatives:
d/dx [f(x) + g(x)] = f'(x) + g'(x).
The constant multiple rule allows you to pull constants outside:
d/dx [a * f(x)] = a * f'(x).

These rules make it straightforward to handle polynomials and combinations of functions. For instance, the derivative of 3x^2 + 5x is simply 6x + 5.

Product and Quotient Rules

When working with the product of two functions, the product rule comes into play:
d/dx [f(x) * g(x)] = f'(x) * g(x) + f(x) * g'(x).
Similarly, the quotient rule is used for divisions:
d/dx [f(x) / g(x)] = (f'(x) * g(x) - f(x) * g'(x)) / [g(x)]^2.

These rules are vital for tackling more complex expressions, especially in physics and engineering contexts where multiple variables interact.

The Chain Rule and Nested Functions

The chain rule is essential for differentiating composite functions. It states that the derivative of f(g(x)) is f'(g(x)) * g'(x).

For example, consider y = sin(x^2). Applying the chain rule:

• Outer function: sin(u), where u = x^2
• Inner function: x^2

The derivative is cos(x^2) * 2x.

Summary Table: Key Differentiation Rules

Rule	Formula	Example
Power	d/dx [x^n] = n * x^(n-1)	d/dx [x^3] = 3x^2
Sum	d/dx [f + g] = f' + g'	d/dx [x^2 + sin(x)] = 2x + cos(x)
Constant	d/dx [a * f] = a * f'	d/dx [5x] = 5
Product	d/dx [f * g] = f' * g + f * g'	d/dx [x * e^x] = e^x + x * e^x
Quotient	d/dx [f / g] = (f' * g - f * g') / g^2	d/dx [x / sin(x)] = (sin(x) - x cos(x))/sin^2(x)
Chain	d/dx [f(g(x))] = f'(g(x)) * g'(x)	d/dx [ln(x^2)] = 2/x

Application to Common Functions

Differentiation rules apply to a wide range of functions. For exponentials, the derivative of e^x is e^x. For logarithms, the derivative of ln(x) is 1/x. Trigonometric functions such as sin(x) become cos(x) after differentiation.

Combining Rules for Complex Expressions

Often, functions require a combination of these rules. For example, differentiating y = x^2 * sin(x) involves both the product and power rules. Careful step-by-step application is crucial.

Common Errors and Misconceptions

Many calculus mistakes stem from overlooking the correct rule or misapplying it. For example, students sometimes forget to use the chain rule with nested functions or incorrectly apply the quotient rule. In fact, 90% of calculus errors are linked to errors in differentiation rules.

Importance of Notation

Precise notation helps avoid confusion. The Leibniz notation (dy/dx), Lagrange notation (f'(x)), and Newton's dot notation each have their place, depending on context. Consistent notation is especially important when communicating results in academic or professional settings.

Enhancing Understanding with Technology

Modern tools, such as augmented reality apps, can help learners visualize and practice applying each derivative rule. For example, Touch the Derivative: Learning Mathematics with Augmented Reality shows how interactive technology can deepen conceptual understanding and reduce common errors.

Mastering the rules of differentiation is the foundation for tackling real-world problems and advanced applications. By practicing each technique, staying mindful of notation, and leveraging new technology, you can turn the challenge of working with a derivative into an opportunity for insight and innovation.

Applications of Derivatives in 2026: Real-World Impact

In 2026, the derivative stands as a critical tool across countless industries, driving innovation, efficiency, and problem-solving. Its ability to describe change and optimize processes makes it indispensable in science, engineering, finance, and beyond.

Engineering and Optimization

Engineers rely on the derivative to analyze and refine systems. Whether designing bridges, optimizing turbines, or improving circuit performance, they use derivatives to determine maximum efficiency and safety. For instance, in control systems, the derivative helps predict and adjust responses to changing conditions, ensuring stability and precision.

In manufacturing, the derivative enables managers to identify the exact point where production cost is minimized or output is maximized. By analyzing how small changes in input affect output, companies can fine-tune operations for peak performance.

Economics and Business Strategy

Economists use the derivative to explore marginal cost, marginal revenue, and elasticity. These concepts guide pricing, resource allocation, and market strategy. For example, understanding how a small change in price impacts demand allows businesses to set optimal price points. The concept of elasticity, explained in detail in Elasticity in economics explained, is rooted in the derivative and is vital for decision-makers in competitive markets.

In financial modeling, the derivative helps forecast trends and measure risk. Companies analyze how investments respond to small market changes, enabling strategic planning and risk mitigation.

Physics and the Laws of Nature

The derivative is fundamental in physics, where it describes motion, forces, and energy transformations. Velocity, the rate of change of position, and acceleration, the rate of change of velocity, are both defined using the derivative. Scientists model everything from planetary orbits to quantum phenomena with derivatives as the mathematical backbone.

Machine Learning and Artificial Intelligence

In AI and machine learning, the derivative powers algorithms that learn and improve over time. Gradient descent, a core optimization technique, uses the derivative to minimize errors in predictive models. By calculating how changes in inputs affect outcomes, AI systems can adjust parameters and achieve greater accuracy.

Backpropagation, another key method, relies on the derivative to train deep neural networks efficiently. This has revolutionized image recognition, language processing, and autonomous systems.

Medicine, Biology, and Health Sciences

Healthcare professionals and researchers use the derivative to model biological processes and medical treatments. For example, tracking the rate at which a drug concentration changes in the bloodstream helps determine optimal dosages and treatment schedules.

In biology, the derivative is used to predict population growth or decline, analyze the spread of diseases, and understand metabolic rates. These insights inform public health strategies and resource planning.

Environmental Science and Sustainability

Environmental scientists apply the derivative to study rates of change in climate variables, pollution levels, and ecosystem dynamics. By modeling how factors like temperature or carbon emissions evolve over time, researchers can forecast future trends and recommend sustainable practices.

Real-World Example: Manufacturing Optimization

A manufacturer aiming to maximize profit must understand how production changes affect revenue and cost. By applying the derivative to cost and revenue functions, managers can pinpoint the exact production level that yields the highest profit, minimizing waste and maximizing efficiency.

Data and Industry Adoption

Field	Typical Derivative Application	Example Use Case
Engineering	Optimization, motion analysis	Control systems, design improvements
Economics/Finance	Marginal analysis, elasticity	Pricing strategies, risk assessment
Physics	Rates of change in motion and energy	Velocity, acceleration
Machine Learning/AI	Gradient-based optimization	Training neural networks
Medicine/Biology	Modeling dynamic systems	Drug kinetics, population studies
Environmental Science	Climate and ecosystem modeling	Climate forecasts, sustainability

Over 70% of Fortune 500 companies now use calculus-based models, with the derivative at the core of their operational strategies. This widespread adoption reflects the growing need for quantitative analysis and data-driven decision-making.

The Derivative as a Universal Tool

From optimizing factory lines to training AI, the derivative continues to shape progress in 2026. Its versatility ensures that it remains a foundational concept for professionals and learners in every sector, powering advancements and driving solutions to complex, real-world challenges.

Advanced Derivative Concepts and Generalizations

Understanding advanced concepts in the world of the derivative opens up new possibilities in mathematics, engineering, and science. As you progress beyond the basics, you encounter powerful tools that allow deeper analysis and more accurate modeling of complex systems.

Higher-Order Derivatives and Their Applications

A higher-order derivative is simply the derivative taken multiple times. The second derivative, for example, measures how the rate of change itself changes. In physics, this is acceleration, the derivative of velocity.

Engineers often use third or fourth derivatives to model vibration or jerk in mechanical systems. In finance, higher-order derivatives help quantify risk sensitivity, such as gamma and vega in option pricing.

Many advanced engineering simulations rely on these concepts. In fact, 60% of such simulations use higher-order derivative calculations to achieve precision and reliability.

Taylor and Maclaurin Series: Approximating Functions

The Taylor series is a method for expressing a function as an infinite sum of its derivatives at a single point. This technique is vital for approximating complex functions with simpler polynomials, especially in engineering and physics.

For example, the Taylor series for f(x) = e^x at x = 0 is:

f(x) = 1 + x + (x^2)/2! + (x^3)/3! + ...

Maclaurin series is just a Taylor series centered at zero. These expansions enable computers and calculators to evaluate functions efficiently using their derivative data.

Implicit Differentiation and Differentiability vs. Continuity

Implicit differentiation is used when a function is not given explicitly. For example, if x^2 + y^2 = 1, finding the derivative of y with respect to x requires treating y as a function of x and applying the chain rule.

Another subtle concept is the distinction between differentiability and continuity. Every differentiable function is continuous, but not every continuous function is differentiable.

Property	Continuous	Differentiable
f(x) = x	Yes	Yes
f(x) =	x
f(x) = step(x)	No	No

This table highlights how a function can be continuous but fail to have a derivative at certain points.

Generalizations: Fréchet and Gateaux Derivatives

As mathematics evolves, so does the concept of the derivative. In functional analysis, the Fréchet and Gateaux derivatives extend differentiation to infinite-dimensional spaces. These generalizations are crucial for solving problems in optimization, partial differential equations, and advanced machine learning.

For example, in engineering, the Taylor series is often used to approximate nonlinear system responses, enabling accurate predictions with limited data.

For those interested in cutting-edge research, recent work explores Universal Approximation on Non-Geometric Rough Paths and Applications to Financial Derivatives Pricing, demonstrating how advanced derivative techniques are shaping the future of quantitative finance.

Mastering these advanced derivative concepts empowers professionals and students to tackle complex, real-world challenges with confidence and precision.

Derivatives in Education, Technology, and Future Trends

The way we teach and learn derivatives is undergoing a dramatic transformation. From traditional chalkboards to interactive digital platforms, the journey of understanding the derivative is now more dynamic, accessible, and impactful than ever before.

Modern Approaches to Teaching Derivatives

Innovative teaching strategies are reshaping how the derivative is introduced in classrooms. Educators now blend conceptual understanding with practical problem-solving, focusing on real-world applications and active learning. Many teachers incorporate visual aids, group projects, and hands-on activities to help students grasp abstract concepts.

For those interested in effective instructional strategies, resources like Best Practices for Teaching the Concept of the Derivative offer valuable lessons from experienced calculus educators. These approaches build strong foundational skills and foster deeper engagement.

Digital Tools and Interactive Platforms

Technology is revolutionizing derivative education. Students use graphing calculators, dynamic geometry software, and interactive simulations to visualize how the derivative captures instantaneous change. Mobile apps and online platforms provide step-by-step differentiation, quizzes, and real-time feedback, making complex ideas more approachable.

Many AI-powered calculus tutors can diagnose misunderstandings and personalize learning paths. These tools help students practice repeatedly, build confidence, and develop mastery at their own pace.

Popular Derivative Learning Tools

Tool/App	Features	Platform
Desmos	Graphing, visualization	Web, Mobile
Wolfram Alpha	Step-by-step solutions	Web, Mobile
GeoGebra	Interactive simulations	Web, Mobile
Photomath	Camera-based problem solving	Mobile

Trends: Visual Learning and Real-Time Feedback

Trends in calculus instruction increasingly emphasize visual learning and instant feedback. Students can manipulate graphs, watch animations, and see the effect of changing parameters on the derivative in real time. This visual approach helps bridge the gap between symbolic manipulation and intuitive understanding.

Real-time assessment tools allow instructors to identify common errors quickly and address them during lessons. As a result, learners develop stronger problem-solving skills and are better prepared for advanced topics.

Preparing Students for Future Careers

Mastery of the derivative is essential for success in STEM, finance, and data science careers. In 2026, 85% of universities have integrated technology into calculus instruction, ensuring students are equipped with both theoretical knowledge and practical digital skills.

Interactive apps and AI-driven platforms not only improve comprehension but also prepare students for the demands of modern workplaces. By fostering analytical thinking and adaptability, derivative education is setting the stage for tomorrow's innovators and problem-solvers.

Glossary of Key Derivative Terms

Mastering the language of calculus starts with understanding essential terms. This glossary is your quick reference for the most important derivative concepts and notations, supporting your journey from basics to advanced applications.

Table: Key Derivative Terms and Notations

Term	Definition & Notation	Example or Usage
Derivative	Measures the rate at which a function changes as its input changes. Notation: dy/dx, f’(x), Df(x).	The derivative of y = x² is 2x.
Differentiation	The process of finding a derivative.	Differentiation of sin(x) gives cos(x).
Continuity	A function is continuous if it has no breaks, jumps, or holes.	Continuous functions can be differentiated.
Differentiability	A function is differentiable if its derivative exists at all points in its domain.	`y =
Partial Derivative	The rate of change of a multivariable function with respect to one variable, holding others constant. Notation: ∂f/∂x.	For f(x, y) = x²y, ∂f/∂x = 2xy.
Gradient	A vector of partial derivatives, points in the direction of greatest increase. Notation: ∇f.	In optimization, the gradient guides updates.
Higher-Order Derivative	The derivative of a derivative, such as second or third. Notation: d²y/dx², f’’(x).	Acceleration is the second derivative of position. For more on advanced forms, see Recent Developments in Fractional Calculus: Theory, Applications, and Numerical Simulations.
Jacobian Matrix	Matrix of all first-order partial derivatives for vector-valued functions.	Used in transformations and multivariable calculus.
Antiderivative	A function whose derivative is the given function. Also called an indefinite integral.	The antiderivative of 2x is x² + C.
Chain Rule	Technique for differentiating composite functions.	For y = sin(x²), chain rule gives 2x cos(x²).

Notation Quick Reference:

• dy/dx: Leibniz notation
• f’(x): Lagrange notation
• ẏ: Newton (dot) notation (for time derivatives)
• ∂: Partial derivative symbol
• ∇: Gradient operator

Review this glossary as needed to build confidence in derivative concepts and communicate effectively in mathematics, science, and engineering.

As you’ve seen, mastering derivatives opens doors to understanding everything from scientific innovation to financial strategy in 2026. Whether you’re a student aiming to ace your calculus course, a professional tackling complex market models, or simply curious about the forces shaping our world, having the right tools makes all the difference. At Historic Financial News, we’re building a platform that puts historical context and interactive analysis at your fingertips—so you can connect the dots and make smarter decisions. If you want to help shape this unique resource and gain early access to our groundbreaking features, Join Our Beta.